Sep 30, 2019
Negative Rates Are Rewriting the Rules of Modern Finance
, Bloomberg News
(Bloomberg) -- Negative interest rates have quite literally broken one of the pillars of modern finance.
As economists and central bankers weigh the pros and cons of sub-zero rates and their impact on the world, traders have been contending with a rather more mundane, but fundamental issue: How to price risk on trillions of dollars of financial instruments like interest-rate swaps when their complex mathematical models simply don’t work with negative numbers.
Out are certain variations of the Black-Scholes model, the framework that allowed derivatives to flourish in the past four decades. In are a hodgepodge of approximations and workarounds, including one dating to the 19th century.
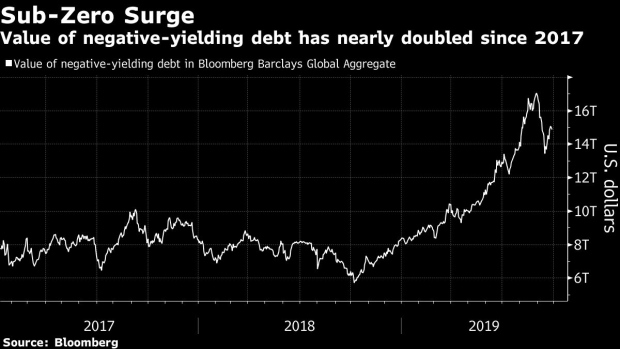
Granted, the current state of affairs is more a nuisance than a serious problem. And it’s one that has been largely confined to Europe and Japan. But with sub-zero interest rates becoming a long-term economic feature and the number of negative-yielding bonds reaching $15 trillion, it’s an issue more and more traders, particularly in the U.S., are trying to wrap their heads around.
“I was quite surprised that I’ve started getting questions from U.S. clients wondering, ‘What’s the impact of negative rates? What are the mathematics?’” said Sphia Salim, a London-based rate strategist at Bank of America.
The issues are most apparent in the market for interest-rate swaps. (This market allows professional investors to lock in interest rates and lets speculators bet on whether rates on bonds or loans will rise or fall.) That’s because the Black 76 model, the main tool to price options for interest-rate derivatives, and its variants are so-called log-normal forward models.
For those who aren’t math nerds, it can essentially be boiled down to this: the formula breaks because it requires users to calculate a logarithm, and a logarithm of a negative number is undefined, or meaningless.
One option has been to dust off a framework that was first proposed nearly a 120 years ago. Known as the Bachelier model, it’s named after the French mathematician Louis Bachelier, who laid out his approach in his 1900 thesis “Theory of Speculation.” The model is best known for solving the math behind a theory from physics known as Brownian motion (some five years before Albert Einstein did the same in his revolutionary work on thermodynamics), and applying it to finance, according to a 2016 paper by Ian Thomson.
For market participants like Banco Di Credito P. Azzoaglio SpA’s Simone Ligato, its appeal is that it simply works with negative numbers -- at least for vanilla instruments like caps, floors and swaptions.
It comes with a few trade-offs. In a 2017 paper co-written by Ligato, the authors concluded that while Bachelier was “coherent enough” to replace Black 76, certain discrepancies make apples-to-apples valuation comparisons difficult. That’s led to some awkward conversation with clients.
“We have to tell customers when the mark-to-market value goes down, so you can imagine their reaction if you explain to them that it’s due to a model change,” Ligato said in an email.
Kuniyuki Hirai, head of trading for the Americas at MUFG Bank, recalls similar headaches when the Bank of Japan went negative in 2016.
“The tension was pretty high,” he said. “We had a lot of swap agreements with our clients in Tokyo. Nobody knew the BOJ would go negative in advance.”
Hirai says MUFG was lucky its models were built in-house, so they were able to make changes on the fly. Yet for some formulas, the firm just had to wing it.
“We went into the formulas, and instead of having one fair value curve, we installed lower bands that can handle negative spreads,” Hirai said of the firm’s model for options on swaps, or swaptions. “We tried to analyze the possibilities, but to be honest we didn’t have a very concrete number.”
Derivatives traders in equities, on the other hand, have it relatively easy by comparison. While their version of Black-Scholes is capable of accepting negative inputs, many have built-in limits on them. So for those, it’s more a matter of software reprogramming. For example, if you try to enter a negative risk-free rate into this online version, here’s what you get:
Tweaking the code, however, doesn’t solve all the issues that go along with negative rates. Pier Giuseppe Giribone, a financial engineer at Banca Carige SpA, points out that sub-zero risk-free rates can cause “approximation errors” for certain kinds of American-style options, which may lead them to become mispriced compared with those used in Europe.
Take an American call option on a stock without dividends, for example. Its value will “only equal the European option when the risk-free rate is positive,” said Giribone, who co-wrote a paper on the subject. “Many automatic pricing systems fail to calculate the right fair value in that scenario.”
For exotic contracts, traders need to turn to more complicated models. One is the Hull-White model, which is more accurate and better able to implement market information, but is also difficult to calibrate.
Oh, and you’ll also want to have your favorite quant on speed dial. That’s because Hull-White needs to be run in a programming language like MATLAB or R, rather than in Excel like Bachelier. And cross fingers that your counterparty has the same inputs, or else there could be a lot of back and forth.
“It’s more difficult for a trader to check the price of an option with their counterparty,” Giribone said.
--With assistance from Anchalee Worrachate.
To contact the reporter on this story: Brandon Kochkodin in New York at bkochkodin@bloomberg.net
To contact the editors responsible for this story: David Gillen at dgillen3@bloomberg.net, Michael Tsang, Larry Reibstein
©2019 Bloomberg L.P.